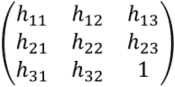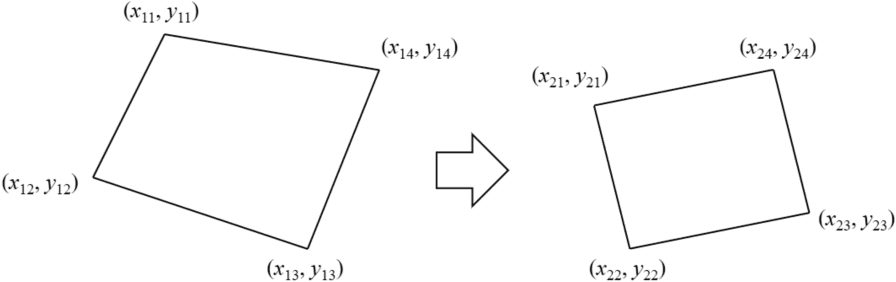
四角形から四角形への変換はホモグラフィー変換行列(射影変換行列)で表現できる.四角形1の頂点(x11,y11)と四角形2の頂点(x21,y21)が対応しており,四角形2の頂点(x12,y12)と四角形2の頂点(x22,y22)が対応しており,四角形1の頂点(x13,y13)と四角形2の頂点(x23,y23)が対応しており,四角形1の頂点(x14,y14)と四角形2の頂点(x24,y24)が対応しているものとする.このとき,四角形1から四角形2へ変換する行列を求めたい.

四角形1の頂点(x1,y1)から四角形2の頂点(x2,y2)への変換は以下に示すようにホモグラフィー変換(射影変換)で表すことができる.
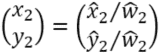
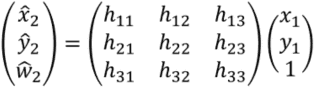
これを式変形すると以下のようになる.
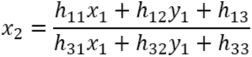
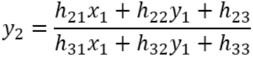
h11,h12,...,h33からなる3×3のホモグラフィー行列(射影行列)をスケール倍しても同じ変換を表す.一意にホモグラフィー変換行列(射影変換行列)を表すため,以下のように,行列の要素のどれか一つの値を固定する.
![]()
これを先程の式に代入し,式変形すると以下のようになる.
![]()
![]()
上の2つの式をベクトル演算で表現すると以下のようになる.
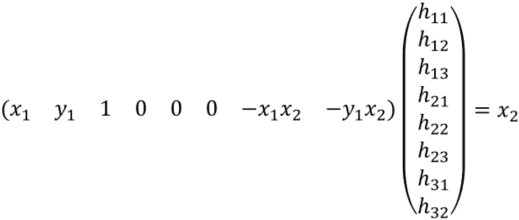
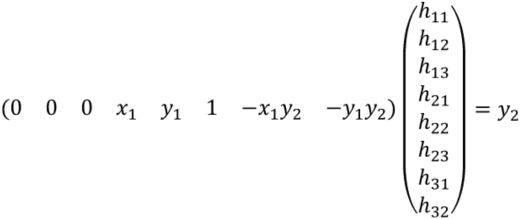
四角形は頂点が4つある.全ての頂点を上の式で表現し,それを並べて行列で表現した式が以下である.

よって,左辺にある8×8行列の逆行列を計算すればホモグラフィー変換行列の各要素が求まる.
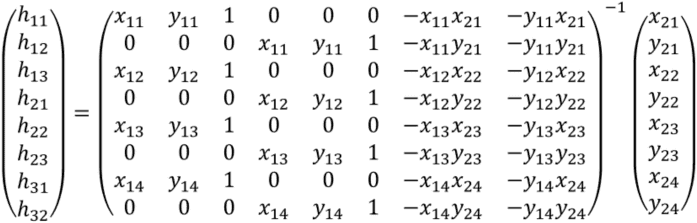
得られたパラメータをもとに,以下のホモグラフィー変換行列が得られる.