三次元空間中に(x,y,z)座標を持つ点群が分布しており,その点群に最もよく当てはまる平面を求める方法を紹介する.
点Pを平面の点とする.平面の単位法線ベクトルをNとする.平面上の点をP0とする.このとき,三次元空間中の平面の方程式は以下のように表すことができる.
![]()
まず,点群の重心を求め,それをP0とする.すなわち,点群P1, P2, ..., PMからP0を以下のように計算する.
![]()
ここで,P0の三次元座標は(x0,y0,z0)と表記する.また,点群の三次元座標は,P1=(x1,y1,z1), P2=(x2, y2, z2), ..., PM=(xM, yM, zM)と表記する.今,解きたい問題は,以下を満たすN=(Nx, Ny, Nz)を求めることである.
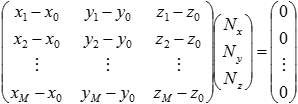
これを以下のように表記する.
![]()
M×3行列Aのrank(階数)は2である.よって,Aを特異値分解したとき,特異値が最小となるときの右特異ベクトルがNの解となる.