主成分分析(PCA)のOpenCVによる実装

主成分分析(PCA: Principal Component Analysis)をOpenCV 2.4.11で実装する方法を紹介します．

int DIMENSION;
int DATANUM;
int EIGENNUM;
cv::Mat data;
cv::Mat mean;
cv::PCA pca;

DIMENSION = /* 各データの次元 */;
DATANUM = /* データの個数 */;
EIGENNUM = DATANUM < DIMENSION ? DATANUM : DIMENSION;

data.create(DATANUM, DIMENSION, CV_64F);
for(int n = 0; n < DATANUM; n++) {
for(int d = 0; d < DIMENSION; d++) {
data.at<double>(n, d) = /* n個目のデータのd次元目の数値 */;
}
}

mean = cv::Mat::zeros(1, DIMENSION, CV_64F);
pca(data, mean, CV_PCA_DATA_AS_ROW, EIGENNUM); // 固有値と基底の数はEIGENNUM個

// pca.eigenvectors.at<double>(n, d)でn個目の基底のd次元目の数値を取得できる
// pca.eigenvalues.at<double>(n)でn個目の固有値を取得できる

上記の例では，平均を引き算せずに主成分分析を適用しています．

主成分分析の実装

以降，さらにもっと具体的に詳しく実装方法を説明します．主成分分析を実感として理解していないのは，実装方法というより，どういう入力データを与えて，その結果どういう出力データが出てきて，その出力データはどういう意味があるのか，といったことがいまいちピンとこないからだと思います．そこで，実際に人工的に作った入力データを使って説明したいと思います．

ここでは，平均を引き算しないで主成分分析を適用する例を示します．コンピュータビジョンの分野では，そのようなケースが多いからです．理由は様々でしょうし，強い理由もあれば，理由が希薄な場合もあるでしょう．問題設定に応じて各自で判断してください．画像の輝度値は常に非負ですので，平均を引くことでマイナスになることを嫌がっているだけの理由の場合もあるかもしれません．データの形は同じでオフセットだけ違う場合，オフセットを平均で表現することはできず，基底で表現することになります．その場合，第１基底でオフセットを表す基底が出てくることが多く，そして，その基底は平均データと同じようなデータであることが多いでしょう．その場合，第１基底で，平均と同じような効果を実現可能なので，平均をわざわざ引き算するのが無駄になると考えるケースもあるでしょう．また，平均を引き算する処理が，論文の数式がややこしくなったり，実装するプログラムがややこしくなったりするので，それを嫌ってというケースもあるかもしれません．また，平均ですと外れ値も平均化されて，平均データに外れ値の要素が目立つことになります．第一基底ですと，基底が全体的にゆがむものの，外れ値が発生した要素が多少目立たなくなるので，それを理由にしているケースもあるかもしれません．

コンピュータビジョンの分野の問題では，データの個数が次元数より少ない場合が多いです．コンピュータビジョンの分野のうち，パターン認識寄りの研究ですとデータの個数が多い問題のほうが多いですが，フォトメトリ寄りの研究ですとデータの個数が少ない問題のほうが多いです．例えば，画像の線形化の研究．例えば，１００万画素の画像を１００枚撮影したとします．１枚の画像の全ての画素の輝度値を一つ一つ縦に並べて１つのデータを作ります．すなわち，データの次元は１００万で，データの個数は１００です．これは一例ですが，このように，データの個数がデータの次元を下回るケースは多いです．

固有値がゼロに近くなる可能性がある場合，主成分分析ではなく特異値分解で計算したほうが安定します．特異値分解で計算する方法は今回のウェブページでは説明を省略します．特異値分解で実装する人は各自で調べて実装してください．

主成分分析のような数値計算では，単精度浮動小数点数（以降，float型と表記）では精度がとてつもなく低く，倍精度浮動小数点数（以降，double型と表記）で計算しないとちゃんとした結果が得られません．しかし，データを保存する場合，double型ほどの精度は必要なく，float型で十分であるので，データを格納する配列はfloat型にしたほうがメモリの効率がよくなります．つまり，データの格納にはfloat型を使い，数値計算の段階ではdouble型を使う，というのが効率がいいわけです．ところがどっこい！数値計算ライブラリによっては，入力データがfloat型で与えられたら，内部の計算もfloat型で計算する，というクソ仕様なライブラリが存在する場合があります．そのため，入力データもdouble型で保存しておいたほうが無難です．メモリが不足するケースが多いので，32bitではなく64bitでコンパイルすることになります．

以降では，Windows 8.1 64bit，Visual Studio Community 2015のVisual C++，OpenCV 2.4.11での例を示します．それ以外の場合は適宜各自で判断してください．

OpenCVとVisual Studioの設定

OpenCVをインストールしてください．インストール方法の説明は省きます．

環境変数PATHに「C:\OpenCV2.4.11\build\x64\vc12\bin」や「C:\OpenCV2.4.11\build\x86\vc12\bin」を追加してWindowsを再起動してください．Visual Studioの「ソリューションプラットフォーム」をx86ではなくx64にしてください．「追加のインクルードディレクトリ」に「C:\OpenCV2.4.11\build\include」を追加してください．「追加のライブラリディレクトリ」に「C:\OpenCV2.4.11\build\x86\vc12\lib」または「C:\OpenCV2.4.11\build\x64\vc12\lib」を追加してください（今はx64で説明しているので後者を追加します）．ディレクトリはインストール時のディレクトリで適宜読み替えてください．

ソースコードに以下を追加してください．

#if _DEBUG
#pragma comment(lib, "opencv_core2411d.lib")
#pragma comment(lib, "opencv_highgui2411d.lib")
#pragma comment(lib, "opencv_imgproc2411d.lib")
#else
#pragma comment(lib, "opencv_core2411.lib")
#pragma comment(lib, "opencv_highgui2411.lib")
#pragma comment(lib, "opencv_imgproc2411.lib")
#endif

#include <opencv2/opencv.hpp>

ファイル形式

入力と出力のファイル形式はカンマ区切りのCSVファイルとします．なお，以降のサンプルプログラムでは，strtok関数を利用してファイルを読み込んでいます．strtok関数はCSVファイルの中に空欄があると読み飛ばしてしまいます．空欄をつくらず，全ての要素（以降，セルと表記）に何かしらの文字列や数値を書くようにしてください．余裕があればstrtok関数を使わないやり方でプログラムを作成してみてください．

0行0列にデータの個数，0行1列にデータの次元が書かれています．1行目以降がデータです．0列目と1列目は無視して，2列目以降がデータです．なお，このウェブページでは，番号は１からではなく０からつけるものとして表記します．「0番目」なんていう言葉は日本語として間違っていますが，実際に実装する学生が添え字を間違えて実装してしまわないように念のためこのような表記にしています．

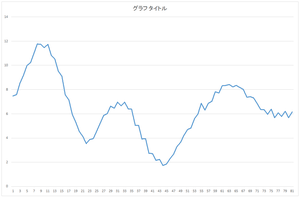
このファイルを使って説明します．データの個数は30，データの次元は81です．

input.csv

		・・・
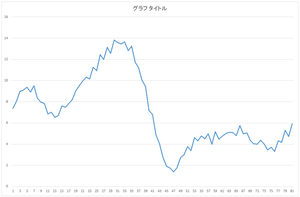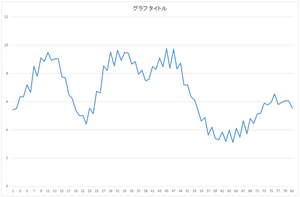
0番目のデータ	1番目のデータ	・・・	29番目のデータ

なお，このウェブページのグラフは縦軸が揃っていなかったり，論文に載せられるような表現をしていなかったりします．実際のCSVファイルをダウンロードして各自で実際の数値を確認してください．

プログラム

正規直交基底

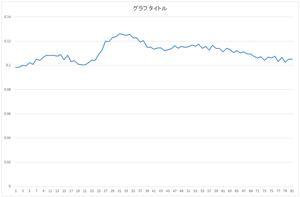
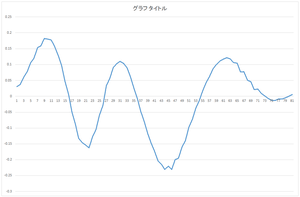
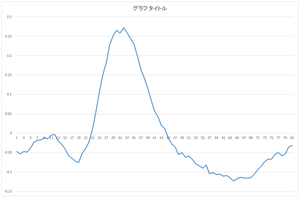
求まった固有ベクトル（主成分）（以降，正規直交基底と表記）はeigenvector.csvというファイルに出力されます．今回の場合は，基底の個数は30，次元は81です．

eigenvector.csv


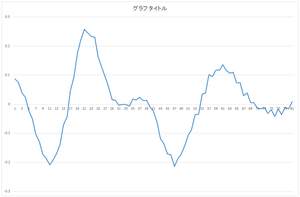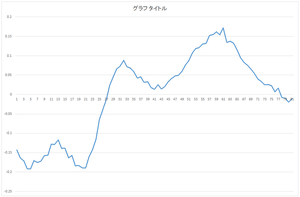
0番目の基底	1番目の基底	2番目の基底	3番目の基底
		・・・
4番目の基底	5番目の基底	・・・	29番目の基底

固有値とスクリープロットと累積寄与率

求まった固有値はeigenvalue.csvというファイルに出力されます．OpenCVのPCA関数では，ちゃんと固有値が降順になるように固有値と固有ベクトルが出力されます．数値計算ライブラリによっては，降順に並び替えないまま出力するライブラリもあるので，注意してください．

eigenvalue.csv

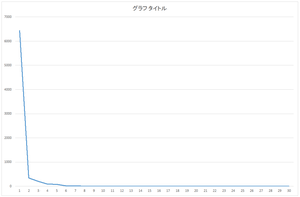
スクリープロット

	固有値	累積寄与率（％）
0	6436.944	89.6066
1	334.7164	94.266
2	202.1589	97.0802
3	92.20386	98.3638
4	81.9489	99.5046
5	12.75018	99.682
6	8.279398	99.7973
7	7.02354	99.8951
8	1.859	99.921
9	0.81758	99.9323
・・・	・・・	・・・
29	0.024546	100

なお，このウェブページの数値は有効数字の桁数などは厳密に考えていないような表現をしています．

本当に正規直交基底なのか

実際に得られた基底はちゃんと正規直交基底になっているのでしょうか．もちろん，数値計算ライブラリが正しく計算しているに決まっています．しかし，プログラマが作ったバグによって，例えば，添え字がずれてしまったり，行と列を間違えていたり，ファイル入出力でfloat型/double型を間違えたり，関数の呼び出し方を間違えていたり，など，人為的なミスにより正規直交基底が正しく出力されていない可能性はあります．

eigenvector.csvの0番目と1番目の基底を検証してみましょう．

0番目の基底	0.098284	0.098572	・・・	0.105024
1番目の基底	0.03047	0.037314	・・・	0.005358

0番目の基底の長さの２乗を計算してみましょう．つまり，0番目の基底と0番目の基底の内積を計算します．
0.098284*0.098284 + 0.098572*0.098572 + ... + 0.105024*0.105024 = 1
計算結果は１です．正規化されていますね．長さは１です．

0番目の基底と1番目の基底の内積を計算してみましょう．
0.098284*0.03047 + 0.098572*0.037314 + ... + 0.105024*0.005358 = -4.2E-07
計算結果は0です．内積が0ということは，0番目の基底と1番目の基底は直角に交わっていることを意味しています．
ところで，実際の計算結果は10の-7乗ぐらいのオーダーであり，0ではありません．数値計算誤差があるので完全に0に一致するとは限りません．10の-7乗であれば十分小さな値ですので，正しく計算されたと判断していいでしょう．
なお，上記の計算はCSVファイルで出力された値を使っています．実際に計算によって得られたdouble型の値を使って計算すれば，かなり0に近い値になると思います．
そもそも，このプログラムですとCSVファイルを出力するとき小数点以下６ケタ程度の数値でしか出力していません．もっと桁数を多くして出力するべきです．また，さらに精度が必要ならば，アスキー形式のファイルとして出力するのではなく，バイナリ形式のファイルとして出力するべきです．

これを30個の基底同士で，30×30の組み合わせ全てで計算すれば，正規直交基底なのかどうかが確認できます．

係数とデータの再構成と次元削減（データベースに含まれるデータ）

正規直交基底の線形和でデータを表現することができます．なお，そのための係数ですが，基底は長さが１でお互い直交しているので，データと基底との内積を計算すれば，それが係数になります．

input.csvのデータの一つを使って説明します．

0番目のデータ

7.476484

7.588744

・・・

6.170647

0番目のデータ

eigenvector.csvの基底を使います．

0番目の基底	0.098284	0.098572	・・・	0.105024
1番目の基底	0.03047	0.037314	・・・	0.005358
・・・	・・・	・・・	・・・	・・・
29番目の基底	0.023033	0.035938	・・・	0.020174

まず，データと基底0との内積を計算してみましょう．
7.476484*0.098284 + 7.588744*0.098572 + ... + 6.170647*0.105024 = 57.6941
次に，データと基底1との内積を計算します．これを基底29まで計算します．

係数0	57.6941
係数1	20.21016
・・・	・・・
係数29	0.417814

つまり，このデータは，基底0を57.6941倍したものと，基底1を20.21016倍したものと，…，と基底29を0.417814倍したものを足し合わせたもの，ということになります．

実際に確認してみましょう．以下，再構成したデータをオレンジ色の線で表しています．比較のため，元のデータを青色の線で表しています．

まずは，基底0を57.6941倍したものを見て見ましょう．

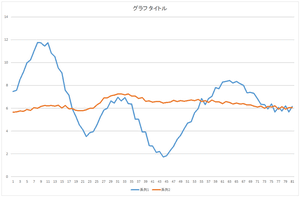=57.6941×

上下の位置は近いですが，データの形がかなり違っていますね．

では次に，基底0を57.6941倍したものと，基底1を20.21016倍したものを足したものを見て見ましょう．

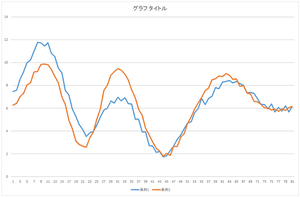=57.6941×

+20.21016×

おっ！一致しているとは言いがたいものの，山と谷の位置はかなり相関が高いですね．

では，これにさらに基底2を-6.59638倍したものを足してみましょう．

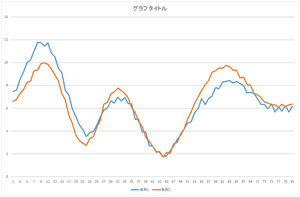	=57.6941×		+20.21016×
	-6.59638×

３つある山のうち，真ん中にある山が近づいてきましたね．

では，これにさらに基底3を-2.05588倍したものを足してみましょう．さらに基底4を-8.48551倍したものを足してみましょう．さらに基底5を-0.81974倍したものを足してみましょう．


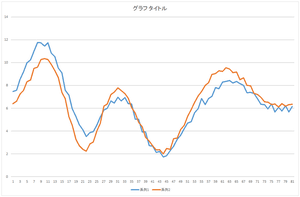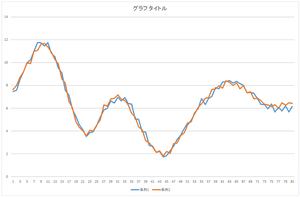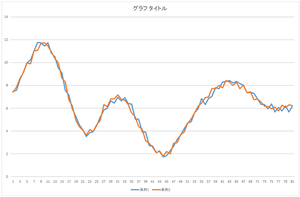基底４つの線形和	基底５つの線形和	基底６つの線形和

おっ！基底５つの線形和でこのデータを表現できますね．もうほとんど一致しているようなものです．57.6941，20.21016，…，-8.48551，という５つの数値だけでこのデータを表現できるわけですね．本来81次元ベクトルは81個の数値で表現するものなのに．次元圧縮（次元削減）ができたわけです．とはいえ，基底５つのデータが必要となってきますが．

でも，これが全てのデータでも同様な性質を持つわけです．つまり，基底５つは共通データとして利用できるわけです．元々のデータは81次元×30個，つまり，2430個の数値で表現していました．基底５つのデータ量は，81次元×5個，つまり，405個の数値で表現できます．個々のデータは５つの係数で表現できるので5個×30個，つまり，150個の数値で表現できます．元々は2430個の数値のデータがあったのが，５つの基底だけで表現するようにすると，405+150，つまり，555個の数値のデータだけで表現できるようになるというわけです．上位５つの基底を使った場合の累積寄与率が９９％を超えているので，５つの基底だけでこのデータをほぼ表現できると言っていいというわけですね．

基底１０個，２０個，３０個使った場合も見て見ましょう．


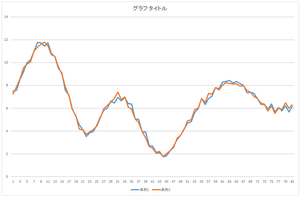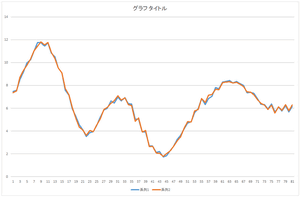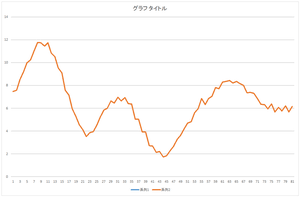基底１０個の線形和	基底２０個の線形和	基底３０個の線形和

全ての基底を使って足し合わせた結果は元のデータと完全に一致しています．これが一致すれば，正しく正規直交基底が計算されたことを意味します．自分のプログラムが正しいかどうかチェックするのに利用できます．

係数とデータの再構成と次元削減（データベースに含まれないデータ）

先程は正規直交基底を計算するために使われたデータベースに含まれているデータを使いました．では，データベースに含まれていないデータはどうでしょうか．もちろん，データベースとは完全に無関係なデータはあまりうまく表現できません．しかし，データベースと同じような性質を持つデータであればある程度表現可能です．

実際にやってみましょう．今回は以下のデータを用意しました．データベースにある30個のデータのどれとも一致していないデータです．しかし，データベースにある30個のデータと同じようなやり方で人工的に作ったデータです．0列目と1列目は無視していただき，2列目以降がデータとなります．

30,data,6.344431462,5.430898881,5.788639826,5.045229125,5.431892473,5.148220769,6.247373877,5.904194559,7.018074794,6.853070842,7.415329243,6.681988468,6.727157704,6.11986334,5.356518341,3.883507699,3.147294817,2.107047233,1.869116159,1.435888089,2.472218576,3.148463328,5.474887965,6.808852152,9.754161136,11.44291821,13.73814761,15.21636521,17.02755852,17.65958085,18.78936127,18.3784868,18.07623842,17.13773537,16.15088152,15.03479419,14.18649566,12.65270032,12.20506825,10.94330218,11.02097082,9.868306121,10.20558999,9.395713825,9.683573142,8.775098307,9.136104211,8.448576259,8.710518542,8.128894893,8.378028257,7.922065916,8.327601559,7.920895667,8.506691436,7.93707303,8.24039303,8.249018074,8.380909421,7.936294965,7.803814733,7.595547706,7.677032829,6.61975181,6.951851616,6.695002513,6.769159695,6.5293568,7.141983556,7.144552264,7.869557545,8.139635591,8.56538665,8.245594894,9.134050718,8.457703754,9.08932824,8.477642682,9.124245036,8.682046072,9.196553879

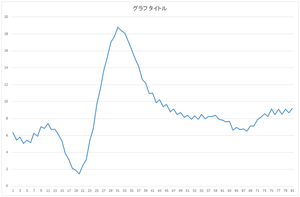
このデータと30個の基底の内積を計算して係数を求めます．

係数0	79.59188
係数1	2.800714
・・・	・・・
係数29	-0.11978

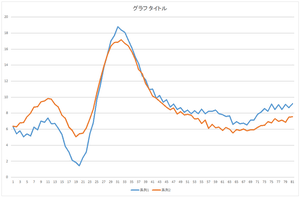
この係数を使って再構成してみましょう．


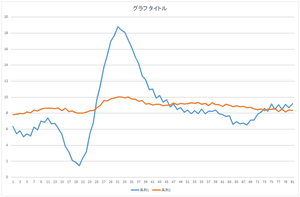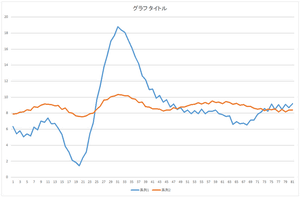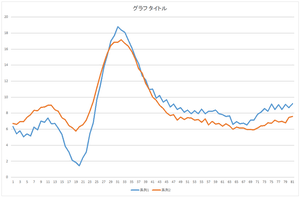基底１個で再構成	基底２個で再構成	基底３個で再構成

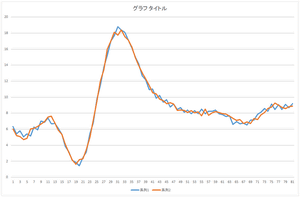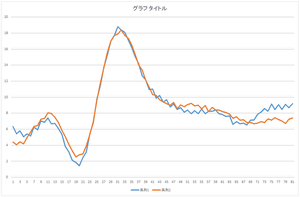
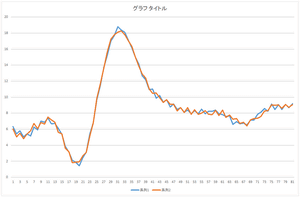
基底４個で再構成	基底５個で再構成	基底６個で再構成

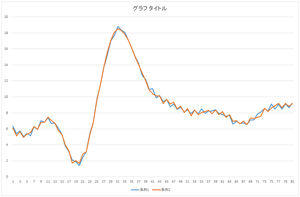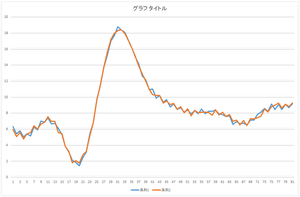
基底１０個で再構成	基底２０個で再構成	基底３０個で再構成

見た感じ，基底６個の線形和で元のデータをほぼ表現できますね．基底３０個を使っても元のデータと完全に一致するデータを表現することは出来ませんね．

欠損データの復元

さて，データベースに含まれないデータとしてgroundtruth.csvというデータを人工的に作って用意しました．

groundtruth.csv

今，以下のように，一部の要素が欠損したデータがあるとします．欠損箇所は分かっているものとします．holedata.csvの0行目が欠損したデータで，1行目は欠損箇所を表します．ここでは，1が有効なデータを表し，0が欠損箇所を表すようなファイルにしています．

holedata.csv

欠損箇所は，コンピュータビジョンの分野の問題設定で言えば，例えば，鏡面反射や影などの外れ値などです．別の例で言うと，画像中の消したい箇所（例えば，テロップがある箇所を指定して，テロップの文字を消したような画像を作りたい，などです．

この欠損箇所を穴埋めできないでしょうか．欠損していない箇所から，正規直交基底に対する係数を求めることができたら．その係数を使ってデータを復元すればいいわけです．

正規直交基底としては，今回は固有値の大きい上位５つの基底を使いましょう．それをeigenvector5.csvというファイルに入れました．

eigenvector5.csv

反復解法

基底を81行5列の行列Aで表し，係数を5次元列ベクトルxで表し，データを81次元列ベクトルbで表すこととしましょう．データを基底の線形和で表すということは，行列の形式だと以下のようにAx=bと表すということを意味します．

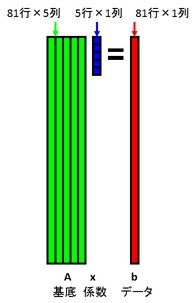
今，データbの一部が欠損しているものとします．欠損箇所には何らかの初期値が入っているものとします．下図では，欠損箇所を黒で表しています．データと基底の内積を計算することで係数を計算します．行列で表現すると，x = A⁺ bを計算することを意味します．ここで，A⁺はAの擬似逆行列を表します．Aは正規直交基底を並べたものであるため，擬似逆行列はAの転置となります．よって，x = A^T bで係数を計算できます．

求めた係数xで基底Aの線形和を計算することにより，データbを復元することができます．b = A xを計算するということです．

元のデータの欠損箇所に先程再構成したデータを埋め込みます．そしてそのデータbを使ってまた係数xを計算します．

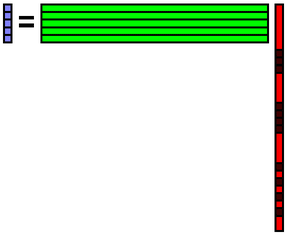
その係数xを使ってデータbを再構成します．

元のデータの欠損箇所に先程再構成したデータを埋め込みます．そしてそのデータbを使ってまた係数xを計算します．

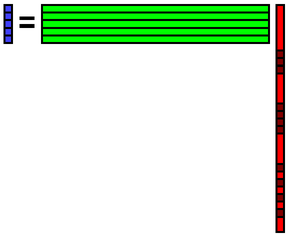
その係数xを使ってデータbを再構成します．

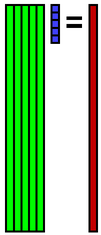
元のデータの欠損箇所に先程再構成したデータを埋め込みます．そしてそのデータbを使ってまた係数xを計算します．

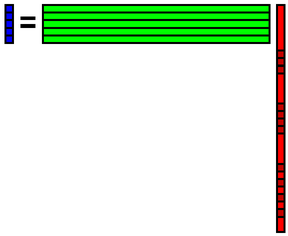
その係数xを使ってデータbを再構成します．

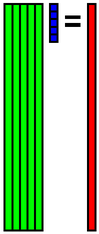
このように繰り返し計算することにより，欠損データを復元することが可能です．欠損箇所がある程度少なく，有効画素がある程度多い場合．

欠損位置を反復計算で修正していくような処理をする場合，この反復解法で解くのがいいと思います．

直接解法

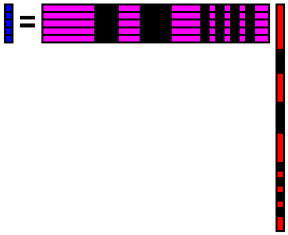
別の解き方を説明します．まず，欠損位置に，データbも基底Aもゼロで埋めます．

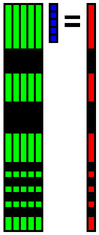
x = A⁺ bを計算することで，係数xを求めます．Aは正規直交基底ではないので，転置行列を使わず，特異値分解などで擬似逆行列を求めます．OpenCVのcv::solve関数の第４引数にcv::DECOMP_SVDを指定すると，x = A⁺ bを求めることができます．

求めた係数xと元の基底Aを使ってデータbを復元することができます．

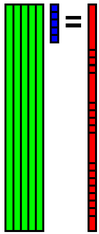
以下にプログラムを示します．このプログラムによって求めた係数がcoefficient.csvで，復元されたデータがfilldata.csvです．

coefficient.csv
filldata.csv


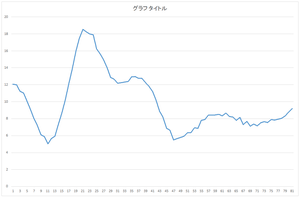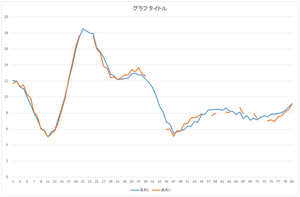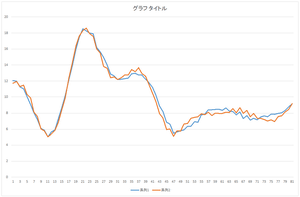復元されたデータ	復元されたデータ（青）と元の欠損データ（橙）	復元されたデータ（青）と真値（橙）

#include "stdafx.h"

#if _DEBUG
#pragma comment(lib, "opencv_core2411d.lib")
#pragma comment(lib, "opencv_highgui2411d.lib")
#pragma comment(lib, "opencv_imgproc2411d.lib")
#else
#pragma comment(lib, "opencv_core2411.lib")
#pragma comment(lib, "opencv_highgui2411.lib")
#pragma comment(lib, "opencv_imgproc2411.lib")
#endif

#include <opencv2/opencv.hpp>
#include <conio.h>

int main()
{
char filename[256];
FILE* fp;
char line[1024];
int EIGENNUM;
int DIMENSION;
cv::Mat eigenorig;
char* context;
cv::Mat data;
cv::Mat hole;
cv::Mat eigenhole;
cv::Mat coef;

// file open
printf("eigenvector file name = ");
scanf_s("%255s", filename, 256);
if (fopen_s(&fp, filename, "rt")) {
    printf("file open error: %s\n", filename);
    printf("push any key\n");
    _getch();
    return 1;
}

// read header
fgets(line, 1023, fp);
sscanf_s(line, "%d,%d", &EIGENNUM, &DIMENSION);
printf("number of eigenvector = %d\n", EIGENNUM);
printf("number of dimension = %d\n", DIMENSION);

// read data
eigenorig.create(DIMENSION, EIGENNUM, CV_64F);
for (int n = 0; n < EIGENNUM; n++) {
    fgets(line, 1023, fp);
    strtok_s(line, ",", &context);
    strtok_s(NULL, ",", &context);
    for (int d = 0; d < DIMENSION; d++) {
      eigenorig.at<double>(d, n) = atof(strtok_s(NULL, ",", &context));
    }
}
fclose(fp);

// file open
printf("data file name = ");
scanf_s("%255s", filename, 256);
if (fopen_s(&fp, filename, "rt")) {
    printf("file open error: %s\n", filename);
    printf("push any key\n");
    _getch();
    return 1;
}

// read data
data.create(DIMENSION, 1, CV_64F);
fgets(line, 1023, fp);
strtok_s(line, ",", &context);
strtok_s(NULL, ",", &context);
for (int d = 0; d < DIMENSION; d++) {
    data.at<double>(d, 0) = atof(strtok_s(NULL, ",", &context));
}

// read data
hole.create(DIMENSION, 1, CV_32S);
fgets(line, 1023, fp);
strtok_s(line, ",", &context);
strtok_s(NULL, ",", &context);
for (int d = 0; d < DIMENSION; d++) {
    hole.at<int>(d, 0) = atoi(strtok_s(NULL, ",", &context));
}
fclose(fp);

// fill zeros
eigenhole.create(DIMENSION, EIGENNUM, CV_64F);
for (int d = 0; d < DIMENSION; d++) {
    if (hole.at<int>(d, 0) == 0) data.at<double>(d, 0) = 0.0;
    for (int n = 0; n < EIGENNUM; n++) {
      if (hole.at<int>(d, 0) == 0) eigenhole.at<double>(d, n) = 0.0;
      else eigenhole.at<double>(d, n) = eigenorig.at<double>(d, n);
    }
}

// calculate coefficients
coef.create(EIGENNUM, 1, CV_64F);
cv::solve(eigenhole, data, coef, cv::DECOMP_SVD);

// reconstruct data
data = eigenorig * coef;

// write coefficients
fopen_s(&fp, "coefficient.csv", "wt");
fprintf(fp, "%d\n", EIGENNUM);
for (int n = 0; n < EIGENNUM; n++) {
    fprintf(fp, "%d,%lf\n", n, coef.at<double>(n, 0));
}
fclose(fp);

// write reconstructed data
fopen_s(&fp, "filldata.csv", "wt");
fprintf(fp, "1,%d\n", DIMENSION);
fprintf(fp, ",,");
for (int d = 0; d < DIMENSION; d++) {
    fprintf(fp, "%lf", data.at<double>(d, 0));
    if (d < DIMENSION - 1) fprintf(fp, ",");
    else fprintf(fp, "\n");
}
fclose(fp);

// finish
printf("push any key\n");
_getch();
return 0;
}

もどる