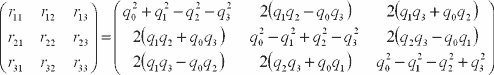
クォータニオン(四元数)を使って回転行列を表すことができますが,ここでは逆に,回転行列が与えられたとき,そこからクォータニオンを計算する方法を説明します.
クォータニオン(4元数, quaternion) q=(q0,q1,q2,q3) ただし |q|=1
クォータニオンから回転行列は以下のように計算できる.
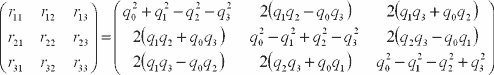
回転行列からクォータニオンに戻す場合.行列rij=aijは回転行列とする.![]() が成り立っている.
が成り立っている.
よって,以下が成り立つ.
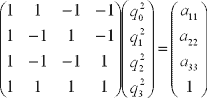
これを解くと,
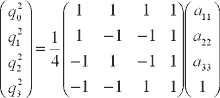
あとは符号を求める.qと-qは同じ回転を表すので,
![]()
とする.
他の符号は以下の通り.
![]()
![]()
![]()
あるいは以下のようにしてもいい.
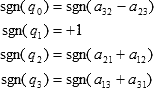
または
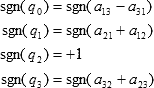
または
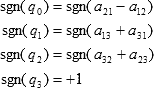
回転行列からクォータニオンに戻すプログラム.
inline float
SIGN(float
x) {return
(x >= 0.0f) ? +1.0f : -1.0f;}
inline float
NORM(float
a, float
b, float
c, float
d) {return
sqrt(a * a + b * b + c * c + d * d);}
q0 = ( r11 + r22 + r33 + 1.0f) / 4.0f;
q1 = ( r11 - r22 - r33 + 1.0f) / 4.0f;
q2 = (-r11 + r22 - r33 + 1.0f) / 4.0f;
q3 = (-r11 - r22 + r33 + 1.0f) / 4.0f;
if(q0 <
0.0f) q0 = 0.0f;
if(q1 <
0.0f) q1 = 0.0f;
if(q2 <
0.0f) q2 = 0.0f;
if(q3 <
0.0f) q3 = 0.0f;
q0 = sqrt(q0);
q1 = sqrt(q1);
q2 = sqrt(q2);
q3 = sqrt(q3);
if(q0
>= q1 && q0 >= q2 && q0 >= q3) {
q0 *= +1.0f;
q1 *= SIGN(r32 - r23);
q2 *= SIGN(r13 - r31);
q3 *= SIGN(r21 - r12);
} else if(q1 >= q0
&& q1 >= q2 && q1 >= q3) {
q0 *= SIGN(r32 - r23);
q1 *= +1.0f;
q2 *= SIGN(r21 + r12);
q3 *= SIGN(r13 + r31);
} else if(q2 >= q0
&& q2 >= q1 && q2 >= q3) {
q0 *= SIGN(r13 - r31);
q1 *= SIGN(r21 + r12);
q2 *= +1.0f;
q3 *= SIGN(r32 + r23);
} else if(q3 >= q0
&& q3 >= q1 && q3 >= q2) {
q0 *= SIGN(r21 - r12);
q1 *= SIGN(r31 + r13);
q2 *= SIGN(r32 + r23);
q3 *= +1.0f;
} else {
printf("coding
error\n");
}
r = NORM(q0, q1, q2, q3);
q0 /= r;
q1 /= r;
q2 /= r;
q3 /= r;