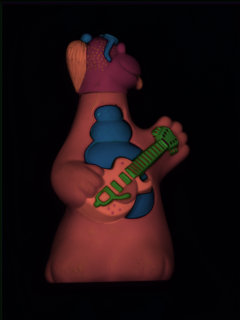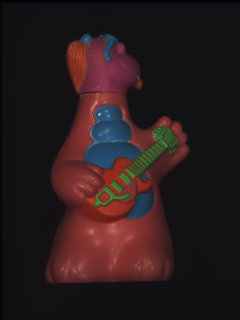
Specular-free画像

Specular-free画像とは

Specular-free imageはTanら[1]が初めに提案した概念である．Tanらが示したのはmaximum choromaticity-intensity空間を使ったものである．私，宮崎，はTanの協力を得て，別の方法でspecular-free imageを生成する方法を提案した[2]．これはM空間と（勝手に）呼んでいる色空間を使ったものである．ここでは，私の方法について説明する．

[1] Go to Robby T. Tan's web page.
[2] Go to Daisuke Miyazaki's Specular-free-image web page.

まず初めにspecular-free画像がどんな画像か示そう．左図が入力画像で，右図がそれに対するspecular-free画像である．


入力画像	Specular-free画像

Specular-free画像の特徴は以下の通りである．

Specularが完全に除去されている
Specular-free画像でのdiffuse albedo（反射率）が実際の物体のdiffuse albedoとは異なる
- 簡単に言うと，物体色が変化してしまうということ
- Hue, Saturation, Intensityで言うと，HueとSaturationは実際の値そのもで，変化しないが，Intensityが実際の値と異なってしまう
- 例えば，緑と赤の物体があったとき，それらは緑と赤の物体になるが，薄緑と深緑の物体があったとき，それは同じ緑の物体になる．
計算方法が実に単純
リアルタイムで計算ができる
テクスチャが複雑な物体に対しても適用可能
画像１枚あれば十分．それ以外は何もいらない．偏光情報もいらないし，データベースもいらないし，複数視点や異なる光源環境の画像などもいらない．光源方向も必要ない．物体の色を知っておく必要もない．Specularの位置を知っておく必要もない．色空間で領域分割や直線フィッティングする必要はなく，計算はピクセルごとに行われる．
Tanら[1]の方法を使えばSpecular-free画像から完全なdiffuse画像を作ることができる

Specular-free imageというネーミングはあまり良くないかもしれない．Specular-free imageには確かにspecularは無いが，specular-free image≠diffuse imageであるからである．Pseudo-diffuse imageと言ったほうがいいのかもしれない．

計算方法

ここでは宮崎の方法を紹介する．まず，ピクセルの値をRGB空間からM空間に変換する．

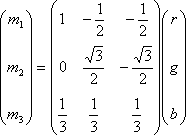
ここで，(r, g, b)がRGB画像の輝度値である．計算はピクセルごとに行われる．上記の計算で得られる(m₁, m₂, m₃)がM画像の輝度値である．実に単純な計算である．

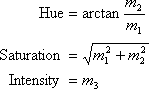
上が(m₁, m₂, m₃)からM空間でのHue，Saturation，Intensityを定義したものである．Hue，Saturation，Intensityは概念的なものを示しているだけで，他の色空間のHue，Saturation，Intensityと同じ値になるわけではない．Hue，Saturation，Intensityを定義するとすれば上のように定義できるという程度のものである．まぁ，もともとHue，Saturation，Intensityは物理的な量ではなく心理的な量なわけだが．Hue，Saturation，Intensityに興味が無ければ上記の計算式は無視していただいて構わない．これらはSpecular-free画像を計算するのには使わない．

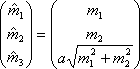
Specular-free画像は上記のように実に簡単に計算できる．ここで，右辺が入力画像で，左辺がSpecular-free画像である．なお，aは任意の値である．a=1とでもしておけばよろしい．ちなみにaが大きいとサチってしまう．aが小さいと黒くつぶれてしまう．

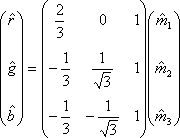
M空間からRGB空間に戻すのは実に簡単である．一番最初の式の逆行列を計算すればいいだけである．結果は上記のようになる．

ちなみに，整数型ではなく浮動小数点型で計算する必要がある．そして，（256段階の場合）全ピクセルのRかGかBの最大値が255になるように正規化してから整数の値にしてRGB画像を表示するといいだろう．もともと，specular-free画像のアルベドは実際のものと異なるので，見やすくなるように正規化してやっても一切問題無い．

ちなみに，Mという文字に特に意味は無い．Miyazakiの頭文字がMだからという理由だけで名付けた．色解析の分野では，R,G,B,C,I,D,S,H,S,V,Y,U,V,Q,Lなどの記号が主に使われていて，Mという文字とバッティングしないだろう，という理由もある．まぁ，CMYのMagentaとバッティングしてしまっているが，コンピュータビジョンの分野ではCMY表色系はほとんど使われることは無いから問題無いだろう．

適用にあたっての注意点

サチったらダメである．つまり，飽和(saturation)が起こってはいけない．RGB輝度値は全てダイナミックレンジ内におさまっていないといけない．256段階のカメラの場合，255の値のピクセルが存在してはいけない．できれば，250以上は存在しないようにしよう．ちなみに，暗すぎても暗電流ノイズの影響でノイズが発生してしまうので画像は十分明るくないといけない．できればハイダイナミックレンジカメラ(256段階を超えるダイナミックレンジのカメラ)を使おう．
カメラは輝度に対して線形でなければならない．すなわち，ガンマ値が１でなければならない．また，カメラのオート機能は全てオフにしておくこと．自動で露出を決める機能なんて絶対オンにしてはならない．シャッタースピードも絞り（アイリス，虹彩，F値）も固定すること．また，デジカメの多くは画像処理を施して人間が見てキレイと感じるように補正してしまっているので，そういうデジカメを使ってはいけない．JPEGなどで保存しているようなデジカメなんて絶対使ってはいけない．必ず観測輝度そのものを出力するようなカメラを使うこと．市販のデジカメの中にはCCDレベルで画像処理を行っているカメラもあり，そういうカメラだとRAWデータですら使い物にならない．ガンマ値を１に設定できない場合は，グレーチャートをシャッタースピードを変えたりして撮影することにより，補正テーブルを作るようにする．その場合でもオート機能は全てオフにする．なお，ピントはあらかじめ合わせておいて，撮影時はピントを動かさないこと．
物体が白い場合は，宮崎の方法でもTanの方法でもspecular-free画像を作ることはできない．
光源は白色でなければならない．ほとんどの光源は白色ではない．人間の視覚は非常に優れており，どんな色の光源下でも心理的に白色光源下での映像と同じものが見えてしまう（カラーコンスタンシー，色恒常性）．カメラはそうはいかない．よって，補正する必要がある．方法は以下の通り．

光源の補正

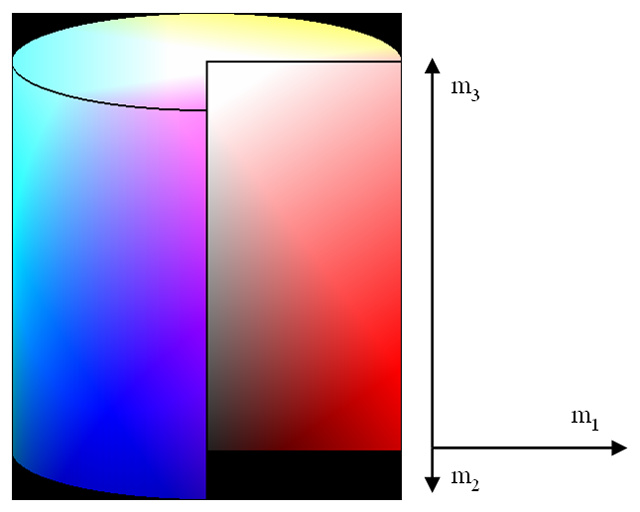
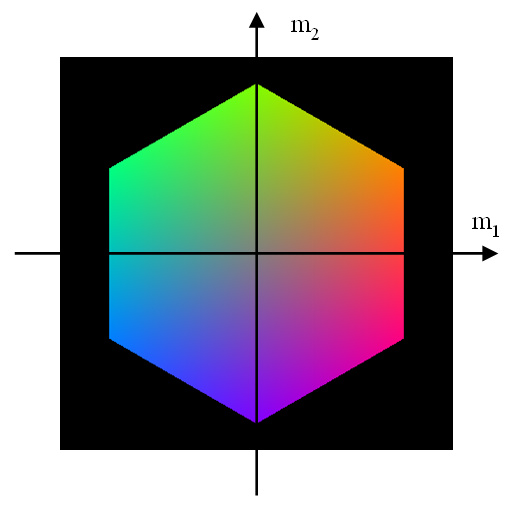
ここでは，白色でない光源下で撮影された画像を白色光源下の画像に直す最も簡単な方法を紹介しよう．要はホワイトバランスを計算するわけである．カメラのホワイトバランス機能を使うという手もあるが，いつでも正しい結果が得られるわけではないので，ここで紹介する方法を使うのが望ましい．なお，光源は複数あっても良いが，全て同じ色でなければならない．なお，同じ色＝同じ製品・型番，であり，異なる製品はどんなに同じ色に見えても微妙に色が異なるので注意してほしい．できれば，ロットナンバーも同じのほうがいいし，製造日からの日数も，購入日からの使用時間も，点灯した時刻も同じほうが良い．相互反射は起こって欲しくないので，物体の近くには他の物体を置いてはならない．色のついた物体からの相互反射は除去できない．黒や白や灰色のアルベドからの相互反射は除去できる．厳密に言うと，色の付いた物体の反射が白（＝灰色・黒）い物体に反射しそしてまたそれが色の付いた物体に反射した場合の相互反射は除去できないが，これはほとんど無視していいだろう．物体の近くには黒いdiffuseな物しか置いてはいけない．黒い＝反射率が低い＝相互反射が起こりにくい．まぁ，相互反射が起こっても心理的にはあまり問題ではないが．相互反射は解析をするPCにとってはやっかいだが，人間にとっては多少の相互反射では，相互反射が起こっていることすら言われないと気づかないものである．Specular-free画像をPCで解析する場合はともかく，specular-free画像を人間に見せるだけなら相互反射が起こっても気にする必要はない．光源は白色でない場合は補正するように，と書いたが，なるべく白色に近い光源を使って補正すること．例えば，完全に赤い光源で照らしてしまうと，RGBのうちRの情報しか手に入らない．

完全に白色なランバート面を持つ平面物体をまず用意する．カメラに付属している場合もある．これはホワイトリファレンスとも呼ばれる．マクベスチャートの白でもいいはずである．石膏の板でもいいだろう．いいのか？白い紙・・・は，できれば避けて欲しい．完全に白でspecularの無い紙ってなかなか見つからない．

実験に使用する光源で完全白色拡散面を照らし，カメラで観測する．このとき，光源も，カメラの設定値も，物体撮影時と全く同じにする．ただし，シャッタースピードは変えても良いし，NDフィルタを付けたりはずしたりも多少問題無いし，絞りを変えてもまぁ問題無いだろう．むろん，全て設定は固定にして，オートで決めたりはしないようにすること．

このときの完全白色拡散面の輝度を下式とする．

これをまず正規化する．

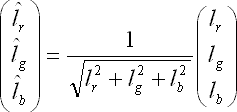
次に，同じ光源，同じようなカメラの設定値で，解析対象とする物体を撮影する．そのときの輝度が以下であるとしよう．

このとき，白色光源下での画像は以下のように計算できる．

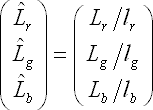
計算時間はなんら難しいことはないことはおわかりいただけるだろう．ステレオとかのキャリブレーションと比べて非常に簡単である．なお，完全白色拡散面のような装置を使わずに，白色光源下の画像を作るアルゴリズムも多数提案されている．"color constancy"もしくは「色恒常性」で検索すれば様々な論文が出てくる．池内研でもいくつかの手法が提案されている．詳しくはこちら．

成功例と失敗例

以下は成功例である．


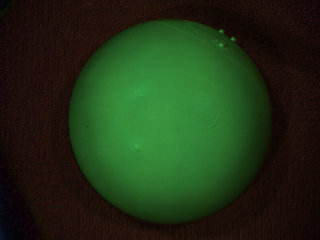入力画像	Specular-free画像（成功）

以下は，光源が白色でなかった場合の例である．


入力画像	Specular-free画像（失敗）

以下は，ガンマ値が１でなかった場合の例である．


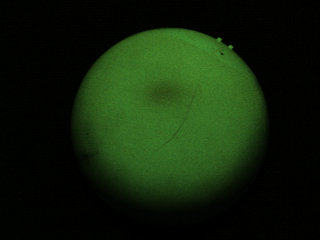入力画像	Specular-free画像（失敗）

Specular-free画像とdiffuse画像との関係

ここでは，speuclar-free画像とdiffuse画像との関係のついて述べる．

Specular-free画像はアルベドが異なるだけ，と述べた．これは，shadingは変わらないということである．これを証明しよう．また，本当にspecularが除去できているかも同時に証明する．

ある画素について考える．

今，光源は白色なのでspecularも白色（NIR仮定）．よってspecularは以下のように表される．

ここで，sはspecularの強さを表す．

Diffuseはランバート面を仮定し，以下のように表すことができる．

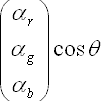
ここで，cosθはランバートの法則で出てくるshadingを表す値である．(α_r, α_g, α_b)がdiffuseアルベドを表す．

よって，RGB輝度は以下のように表される．

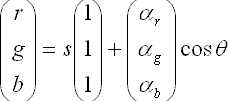
ここからspecular-free画像を計算すると，途中結果は以下のようになり，

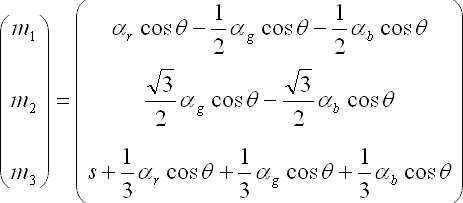
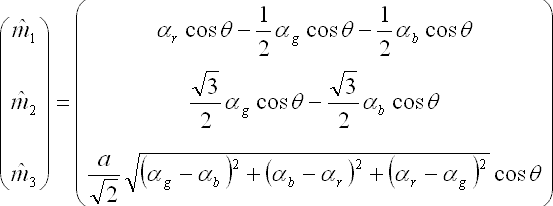
最終的なspecular-free画像のRGB値は以下の通りになる．

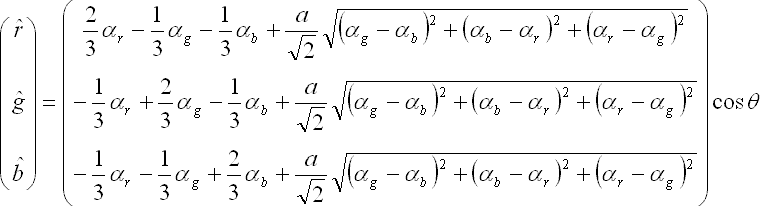
見て分かる通り，

sが消えている．すなわち，specularが完全に除去されている．
cosθがそのまま残っている．すなわち，shadingは正しく残っている．
アルベドが完全に変わってしまっている．

他の色空間は使えるか？

宮崎のM空間以外にも，BajcsyのS空間や，Ohtaの(I₁, I₂, I₃)空間や，Hurvichのopponent responses modelでも，同様の性質を持ったspecular-free画像を計算できる．ただし，その計算方法はここでは紹介しない．自分で考えてみて欲しい．HSV空間などでは上記のような性質を実現することはできない．

[1] R. Bajcsy, S. W. Lee, A. Leonardis, "Detection of diffuse and specular interface reflections by color image segmentation," Int'l J. Computer Vision, Vol.17, No.3, pp.249-272, 1996.
[2] Y. Ohta, T. Kanade, T. Sakai, "Color Information for Region Segmentation," Computer Graphics and Image Processing, Vol.13, pp.222-241, 1980.
[3] L. M. Hurvich, Color Vision, Sinauer Associates, 1981.

応用分野

Tanはspecular-free画像をdiffuse画像を作るための中間結果として利用した．

しかし，speuclar-free画像自体には広範囲な応用が考えられる．その代表的なのが「物体認識」である．

物体認識に置いて，specularの問題が悩みどころであろう．specularが存在すると，物体認識がうまくいかない，という問題があるからである．また，リアルタイム性が要求される場合がほとんどである．そのときにこのspecular-free画像が役に立つ．

「ちょっと待て！Specular-free画像は確かにspecularは無くなるし，リアルタイムで計算できる．でも，specular-free画像はアルベドが実際の物体のアルベドと異なるではないか！それじゃ物体認識はできないだろ！」と思う方もいるだろう．ご安心を．答えは簡単である．全てspecular-free画像だけで処理してしまえばいい．データベース（テンプレート）自体をspecular-free画像にしてしまえばいいわけである．学習理論を使うにしても，学習に使うデータを最初からspecular-free画像にしてしまえばいい．Specular-freeテンプレートをspecular-free画像に対してテンプレートマッチングすればいいというわけである．これならアルベドが異なっても，完全にテンプレートに合致する．

ちなみに，specular-free画像にはshadingが残る．よって，学習した（データベースに入れた・テンプレートにした）specular-free画像と，認識したいspecular-free画像の光源の配置や輝度が異なると，完全には合致しない．

よって，shadingにロバストに物体認識にしたければ，Hue画像を使うという手がある．すなわち，

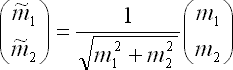
を計算した画像を使えば良い．つまり，一つの画素に（３つの要素ではなく）２つの要素が配置された画像を使ってテンプレートマッチングをすれば良いわけである．

ちなみに，このHue画像は，画素あたりの自由度は１である．Specular-free画像の画素あたりの自由度は２である．

Hue画像をRGB画像に戻したいときは，適当に，例えば以下のように計算する．ただし，以下は256段階の場合．

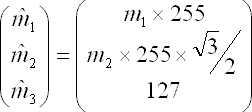
で，上で示した方法でRGB画像に戻せば良い．

なお，specular-free画像からアルベドを求める方法がTanによって提案されているので，そちらを使うという手もある．こちらは反復計算が必要となる．

[1] Go to Robby T. Tan's web page.
[2] Go to CVL Publication web page.

もどる