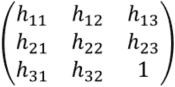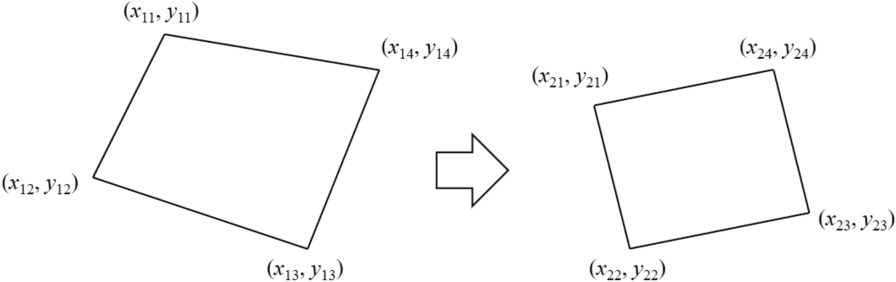
Trasformation from quadrangle to quadrangle can be represented by homography transform matrix (projective transform matrix). Suppose that the vertex (x11,y11) of quadrangle 1 corresponds to the vertex (x21,y21) of quadrangle 2, the vertex (x12,y12) of quadrangle 1 corresponds to the vertex (x22,y22) of quadrangle 2, the vertex (x13,y13) of quadrangle 1 corresponds to the vertex (x23,y23) of quadrangle 2, and the vertex (x14,y14) of quadrangle 1 corresponds to the vertex (x24,y24) of quadrangle 2. Let us calculate the matrix which transforms quadrangle 1 to quadrangle 2.

Transformation from the vertex (x1,y1) of quadrangle 1 to the vertex (x2,y2) of quadrangle 2 can be represeted by homographic trasform (projective transform).
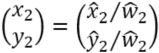
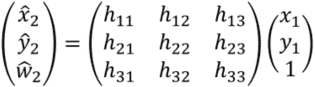
If we change this equation, we obtain the following.
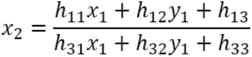
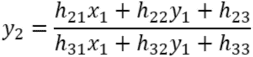
Scaling 3-by-3 homography matrix (projective matrix) consists of h11,h12,...,h33 results in same transformation. In order to uniquely represent the homography transformation matrix (projective transformation matrix), one of the component is fixed as follows.
![]()
Substituting this equation to aforementioned equations, we obtain the followings.
![]()
![]()
Above two equations can be represented by vector representation as follows.
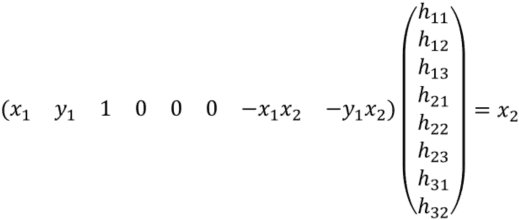
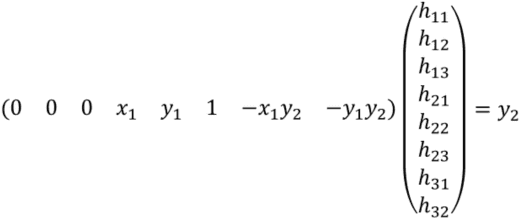
Quandrangle has four vertices. Represeting all vertices with above representation, and concatenating those equations result in the following matrxi representation.

If we calculate the inverse of 8-by-8 matrix shown in the left-hand side of the above equation, we obtain the components of homography matrix.
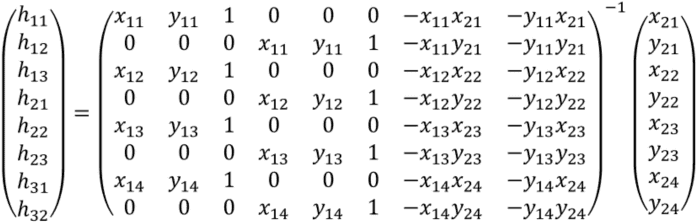
Obtained components give the following homograhpy matrix.