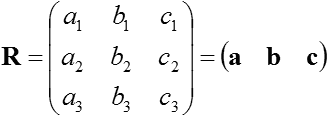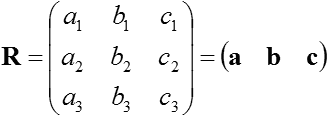
Suppose right-handed 3D coordinates. The determinant of orthogonal matrix is either 1 or -1. Rotation matrix is an orthogonal matrix whose determinat is 1.
Rotation matrix R is a matrix which satisfies the following three conditions.
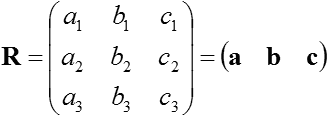
![]()
![]()
![]()
If these three conditions are satisfied, the inverse of R becomes its transpose.
The transpose also satisfies these three conditions.
Suppose a matrix R is a rotation matrix with a small amount of noise. Suppose we want to update R so that it satisfies the condition of rotation matrix. Ignoring the precision, the following procedure is easy to implement.