Matrix orthogonalization and orthonormal basis

Tweet

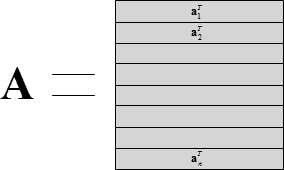
Define square matrix A as follows.

Consider AA^T=I. Here, I is identity matrix.

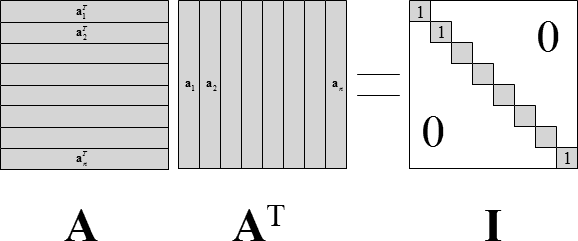
If the above is satisfied then the below also is satisfied, and if the below is satisfied then the above is also satisfied.

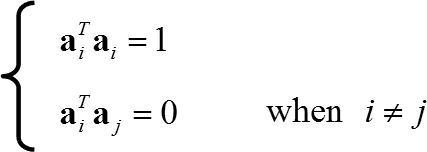
Because AA^T=I is satisfied, A is an orthogonal matrix, so A^TA=I is also satisfied.

If A is an orthogonal matrix, then the rows of A forms orthonormal bases, and the matrix A whose rows are orthonormal bases becomes an orthogonal matrix.

Because both AA^T=I and A^TA=I are satisfied, the columns of A are also orthonormal bases (with different space and axes).

How to orthogonalize the square matrxi A and make the orthogonal matrix B: 1

Use Gram-Schmidt orthonormalization method

One concern is that the result will be different depending on which basis you start calculated

How to orthogonalize the square matrxi A and make the orthogonal matrix B: 2

Calculate the following

This method has to calculate the inverse of the squared-root matrix of the symmetrical matrix (the squared-root matrix of the inverse matrix), using QR decomposition or SVD. So, it is better to use the following two methods instead.

How to orthogonalize the square matrxi A and make the orthogonal matrix B: 3

Calculate the following using QR decomposition

Useful for regular matrix A

How to orthogonalize the square matrxi A and make the orthogonal matrix B: 4

Calculate the following using SVD (singular value decomposition)

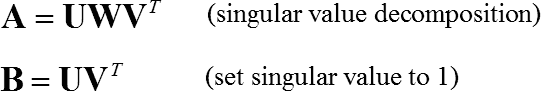
Useful when the matrix A is singular or nearly singular. It is safe when the matrix A is consisted of measurement data.

Back