Convert from rotation matrix to quaternion

Tweet

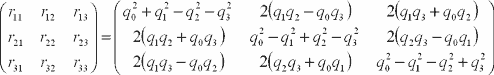
It is well known that rotation matrix can be represented by quaternion. This page explains how to calculate the quaternions when the rotation matrix is given.

Quaternion q=(q₀,q₁,q₂,q₃) where |q|=1

Quaternion to rotation matrix.

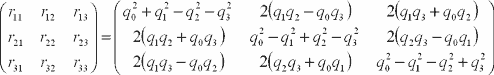
Rotation matrix to quaternion. r_ij=a_ij is rotation matrix.

Therefore,

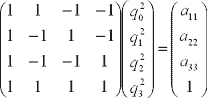
By solving this,

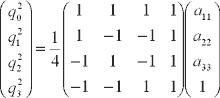
Now let's calculate the sign. q and -q represent same rotation, thus,

Other sign will be as follows.

Another choice is to do as follows.

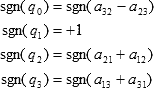
or

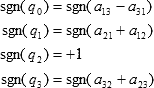
or

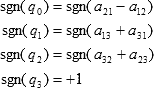
Source code: Convert rotation matrix to quaternion.

inline float SIGN(float x) {return (x >= 0.0f) ? +1.0f : -1.0f;}
inline float NORM(float a, float b, float c, float d) {return sqrt(a * a + b * b + c * c + d * d);}

q0 = ( r11 + r22 + r33 + 1.0f) / 4.0f;
q1 = ( r11 - r22 - r33 + 1.0f) / 4.0f;
q2 = (-r11 + r22 - r33 + 1.0f) / 4.0f;
q3 = (-r11 - r22 + r33 + 1.0f) / 4.0f;
if(q0 < 0.0f) q0 = 0.0f;
if(q1 < 0.0f) q1 = 0.0f;
if(q2 < 0.0f) q2 = 0.0f;
if(q3 < 0.0f) q3 = 0.0f;
q0 = sqrt(q0);
q1 = sqrt(q1);
q2 = sqrt(q2);
q3 = sqrt(q3);
if(q0 >= q1 && q0 >= q2 && q0 >= q3) {
    q0 *= +1.0f;
    q1 *= SIGN(r32 - r23);
    q2 *= SIGN(r13 - r31);
    q3 *= SIGN(r21 - r12);
} else if(q1 >= q0 && q1 >= q2 && q1 >= q3) {
    q0 *= SIGN(r32 - r23);
    q1 *= +1.0f;
    q2 *= SIGN(r21 + r12);
    q3 *= SIGN(r13 + r31);
} else if(q2 >= q0 && q2 >= q1 && q2 >= q3) {
    q0 *= SIGN(r13 - r31);
    q1 *= SIGN(r21 + r12);
    q2 *= +1.0f;
    q3 *= SIGN(r32 + r23);
} else if(q3 >= q0 && q3 >= q1 && q3 >= q2) {
    q0 *= SIGN(r21 - r12);
    q1 *= SIGN(r31 + r13);
    q2 *= SIGN(r32 + r23);
    q3 *= +1.0f;
} else {
    printf("coding error\n");
}
r = NORM(q0, q1, q2, q3);
q0 /= r;
q1 /= r;
q2 /= r;
q3 /= r;

Back