Equation of line in 2D plane and 3D space is shown. Formula of plane is also shown. The distance between point and line is shown. Perpendicular foot from a point to a line is shown. Distance between point and plane is shown. Perpendicular foot from a point to a plane is shown. Mathematical representation of the intersection between two lines in both 2D coordinates and 3D coordinates is also shown.
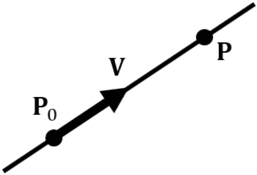
Point ![]() on a line parallel to the unit vecotor
on a line parallel to the unit vecotor ![]() , which passes point
, which passes point ![]() , is represented as follows, using parameter
, is represented as follows, using parameter ![]() .
.
![]()
Denote ![]() ,
, ![]() ,
, ![]() , and reformulate, we obtain the following.
, and reformulate, we obtain the following.
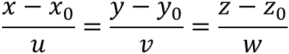
As for 2D, ![]() , namely
, namely 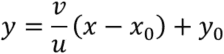 .
.
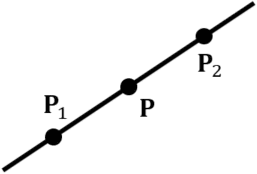
Point ![]() on a line passing point
on a line passing point ![]() and point
and point ![]() is represented as follows, using parameter
is represented as follows, using parameter ![]() .
.
![]()
Denote ![]() ,
, ![]() , and reformulate, we obtain the following.
, and reformulate, we obtain the following.
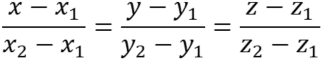
As for 2D, ![]() , namely
, namely 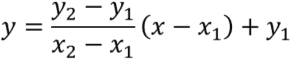 .
.
Point ![]() on a plane including point
on a plane including point ![]() , whose unit normal vector is
, whose unit normal vector is ![]() , is represented as follows.
, is represented as follows.
![]()
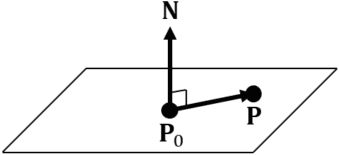
Denote ![]() ,
, ![]() ,
, ![]() , and reformulate, we obtain the following.
, and reformulate, we obtain the following.
![]()
Intersection point ![]() between a line and a perpendicular line from point
between a line and a perpendicular line from point ![]() is represented as follows. Note that
is represented as follows. Note that ![]() must be a unit vector.
must be a unit vector.
![]()
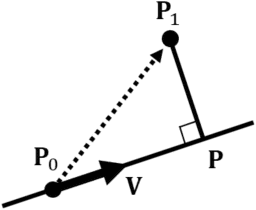
Thus, using the above ![]() , the distance between point and line is represented as follows.
, the distance between point and line is represented as follows.
![]()
Let's think about a line parallel to a unit vector ![]() and passes point
and passes point ![]() . Defining a unit vector
. Defining a unit vector ![]() orthogonal to vector
orthogonal to vector ![]() , the distance between point and line is represented as follows.
, the distance between point and line is represented as follows.
![]()
![]()
By the way, the line is ![]() or
or ![]() .
.
Let's redefine as ![]() ,
, ![]() ,
, ![]() . The line equation becomes following equation.
. The line equation becomes following equation.
![]()
Representing the distance ![]() between point and line using
between point and line using ![]() ,
, ![]() ,
, ![]() results in the following formula.
results in the following formula.
![]()
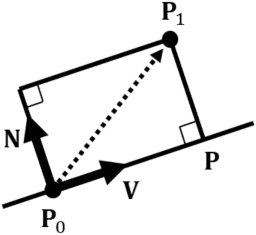
To summarize, the distance between point ![]() and line
and line ![]() , when
, when ![]() holds, is the following.
holds, is the following.
![]()
Intersecting point ![]() between a plane and a perpendicular line from point
between a plane and a perpendicular line from point ![]() is represented as follows.
is represented as follows. ![]() must be unit vector.
must be unit vector.
![]()
The distance between point and plane is represented as follows.
![]()
![]()
By the way, plane equation is ![]() or
or ![]() .
.
Let's redefine as ![]() ,
,![]() ,
, ![]() ,
, ![]() . The plane equation becomes following equation.
. The plane equation becomes following equation.
![]()
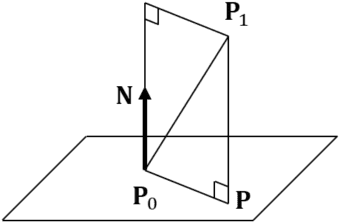
As a result, the distance between point ![]() and plane
and plane ![]() , when
, when ![]() holds, is represented as follows.
holds, is represented as follows.
![]()
Intersection point between line ![]() and line
and line ![]() is as follows.
is as follows.
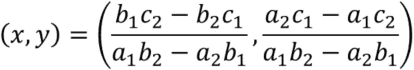
Let's think about a intersecting point ![]() between 3D line
between 3D line ![]() and 3D line
and 3D line ![]() .
. ![]() and
and ![]() are unit vectors. Generally, 2 lines in 3D have no intersecting point.
Let's calculate a point which is the closest to 2 lines.
are unit vectors. Generally, 2 lines in 3D have no intersecting point.
Let's calculate a point which is the closest to 2 lines.
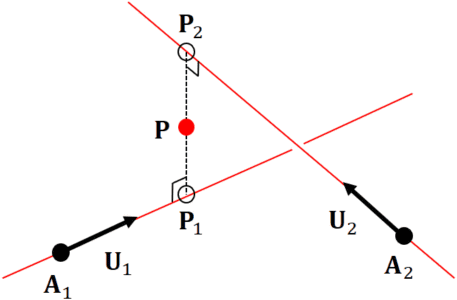
Point ![]() should be close to point
should be close to point ![]() , so
, so ![]() . Point
. Point ![]() should be close to point
should be close to point ![]() , so
, so ![]() . Therefore, the following is derived.
. Therefore, the following is derived.
![]()
Therefore,
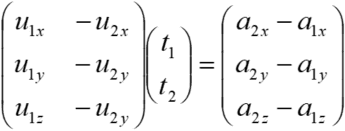
Or,
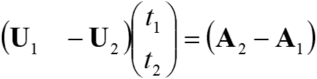
Multiply ![]() from the left for both sides of this equation.
from the left for both sides of this equation.
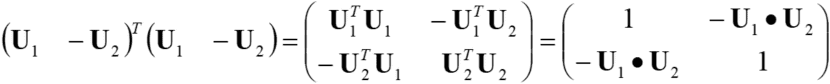
Therefore, the following holds.
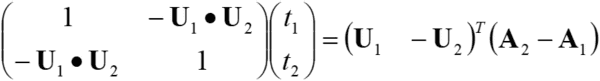
Solving this results in the following.
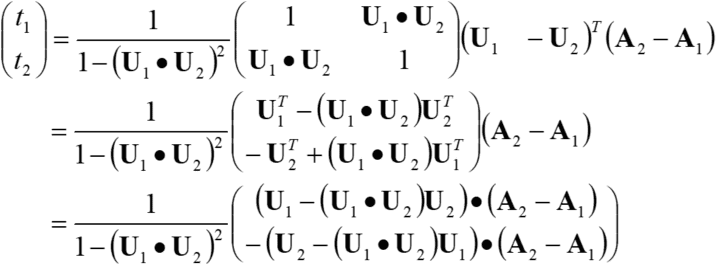
The solution which satisfies both ![]() and
and ![]() as much as possible is
as much as possible is 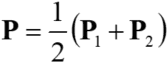 . Substituting the above equation to this equation results in the following
intersecting point.
. Substituting the above equation to this equation results in the following
intersecting point.
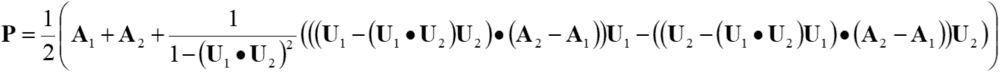
Here, ![]() holds.
holds.
If ![]() , intersecting point exists.
, intersecting point exists.
If ![]() , intersecting point does not exist because 2 lines are parallel.
, intersecting point does not exist because 2 lines are parallel.