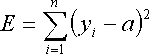
Given data sequence yi(i=1,...,n), and represent as yi=a, the value a independent to i. Thus, minimize
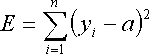
Solution can be found by partial differating E by a and putting "=0" and solve for a. Thus,
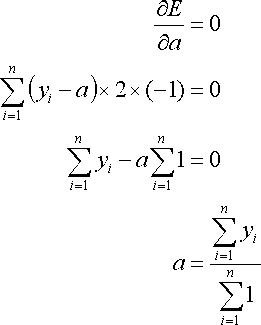
Here, following equation holds.
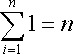
Thus, the required value a is the average of data sequence yi.
For the rest of the page, I omit the subscript i. For example, E and a will now be represented as
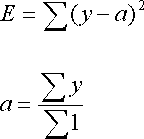
Given data sequence (x,y), minimize E and estimate a and b.
![]()
Partial differentiate E by a and b respectively and setting =0
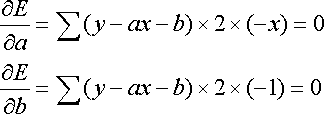
Thus
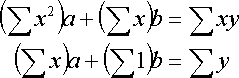
Solution is
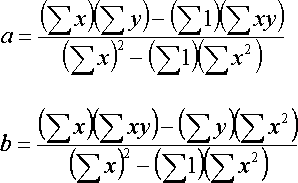
Given data sequence (x,y), and minimize E and estimate a, b, and c.
![]()
Partial differentiate E by a, b, and c respectively and setting =0
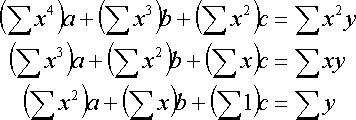
Solution is
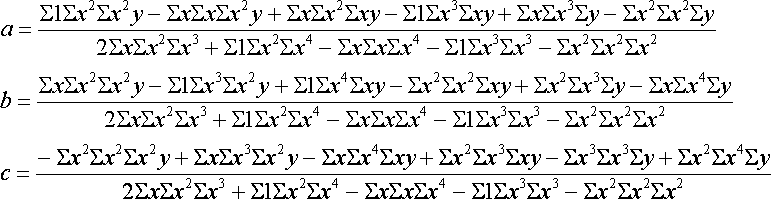
Here
![]()
is
![]()
Same for other sums.
Since ordinary trigonometric functions are non-linear, we cannot solve them explicitly (maybe). We must solve by iteration methods such as Levenberg-Marquardt method.
Given the cycle of trigonometric function, we can explicitly solve the least square problem.
m is known, data sequence (x,y) is given, and we want to apply y=Asinm(x-B)+C to data sequence (x,y). We want to estimate A,B,C. We cannot solve the equation directly (maybe) by least square method due to its nonlinearity. Thus, we use the following relation of trigonometric functions.
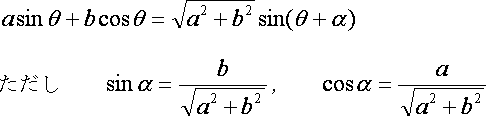
We can solve the least square problem of the following trigonometric function.
![]()
Thus, solve
![]()
and calculate a,b,c and transform them into A,B,C.
a,b,c will be the following.
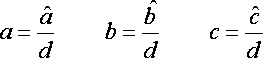
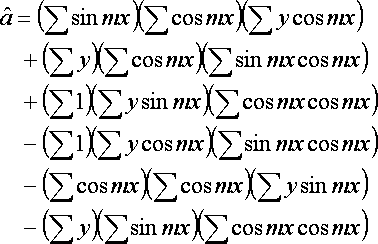
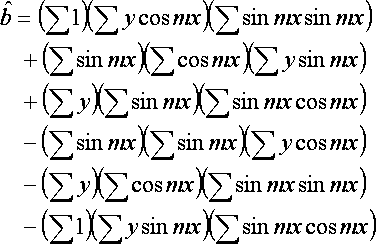
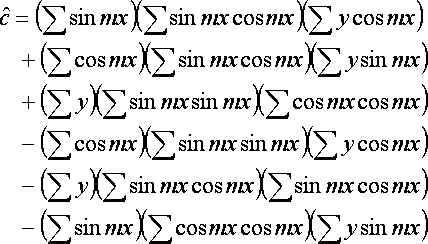
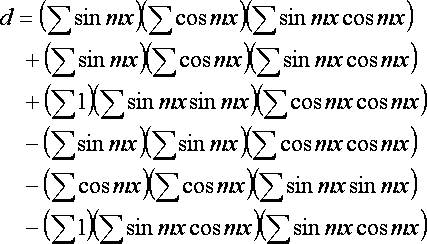
Transformation from a,b,c to A,B,C will be the following.
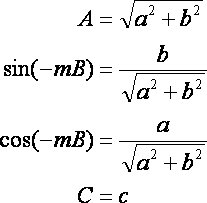
Hey! Wait a minimute! Does this method really solve the problem? There is an ambiguity of estimating phase B! Adding or subtracting the period several times towards B will be also the solution for B. In addition, depending on B, there is an ambiguity of the sign of A! It is impossible to "stablely" solve with linear least squares method!
......some people will think like that. Don't worry. There is no problem. The method "stablely" estimates the parameters.
The point is that we never fit y=Asinm(x-B)+C directly but fit y=asinmx+bcosmx+c. a,b,c are uniquely estimated by solving the least squares method of y=asinmx+bcosmx+c.
Now I will give a proof. What one wants to know is the following question.
Is there any a![]() a' or b
a' or b![]() b' or c
b' or c![]() c' under the following constraint?
c' under the following constraint?
(1) asinx+bcosx+c=a'sinx+b'cosx+c'
If there exists, it means that the method produces many values of a,b,c. Thus, there is an ambiguity in parameter estimation. Transforming (1) will give the following equation.
(2) (a-a')sinx+(b-b')cosx+(c-c')=0
Here, the first and second term can be composed into one sine function.
(3) ![]()
where
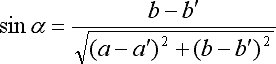
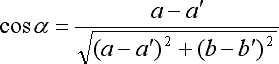
Sine function varies from -1 to 1 depending on x. (3) must hold for all x, thus, the coefficient of sine must be 0. Thus, both two equations below must be held.
(4) ![]()
(5) ![]()
Therefore c=c'.
(6) (a-a')2+(b-b')2=0
Here, both (a-a')2 and (b-b')2 are non-negative. Thus, both (a-a')2=0 and (b-b')2=0 must hold. As a result, a=a' and b=b'.
Now the proof is over, and we know that the method can uniquely estimate a,b,c. The transformation from a,b,c to A,B,C can be calculated by abovementioned formulae. From this transformation, A will always be non-negative. B has an ambiguity with the interval of the period, but you can freely calculate B in any range you like.
By the way, we can prove a=a', b=b', and c=c' only from (2). Why did I synthesize the two trigonometric functions into one function? I thought that someone might think "If we can transform like cosx=sinx+?, a&b&c could not be uniquely solved." Note that there is no such transformation.