行列の直交化と正規直交基底

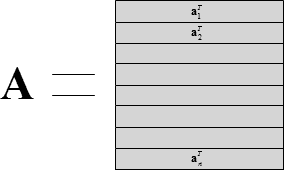
正方行列Aを以下のように表現する

このとき，AA^T=Iを考える．ただしIは単位行列．

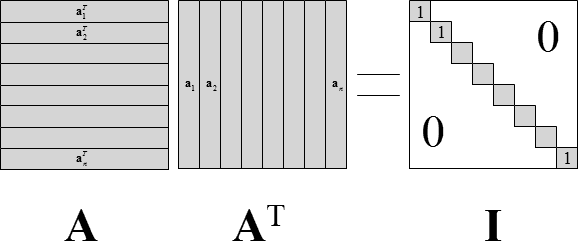
上記が成り立つとき下記が成り立つ，また，下記が成り立つとき上記が成り立つ．

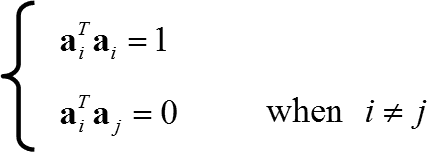
AA^T=Iが成り立つということはAが直交行列であるということでありA^TA=Iも成り立つ．

つまりAが直交行列のときAの各行は正規直交基底となっている，また，Aの各行に正規直交基底を並べた行列は直交行列となる．

AA^T=IもA^TA=Iも成り立つので，このときAの各列も（別の座標軸を持つ）正規直交基底になっている．

正方行列Aを直交化して直交行列Bを求める方法１

Gram-Schmidtの正規直交化法を使う

結果が，どの基底から始めたかによって変わってくるのが難点

以下を計算する

この方法では対称行列の平方根行列の逆行列（逆行列の平方根行列）を計算しないといけないが，それにはQR分解や特異値分解を使う．それならば，以下の２種類の方法を代わりに使ったほうが良い．

QR分解を使って以下のように計算する

正則行列Aに対して有効な方法

特異値分解(SVD)を使って以下のように計算する

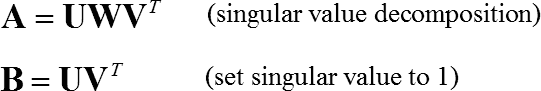
行列Aが特異，または特異に近い場合に有効．実測から得られたデータで行列Aが作られている場合はこの方法を使ったほうが安心．