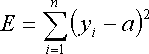
今,データ列yi(i=1,...,n)が与えられて,yi=aといったようにiに依存しない値aで表したい.すなわち,
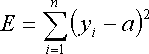
を最小化するaを求めたいわけである.
この解は,Eをaで偏微分して"=0"とおいてaについて解けば求まる.すなわち,
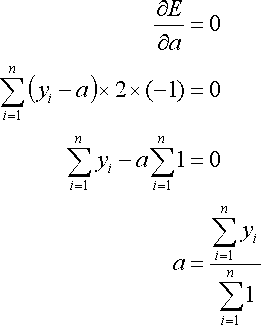
なお,以下が成り立つ.
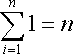
よって,求めるaは,データ列yiの平均値ということになる.
なお,以下,添え字iを省略する.例えば,Eとaは以下のように表記する.
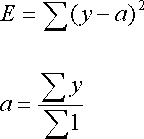
データ列(x,y)が与えられたときに,以下のEを最小化してaとbを求める問題を考えよう.
![]()
Eをa,bそれぞれで偏微分して=0とおくと,
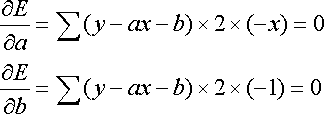
となる.つまり,以下の連立方程式になる.
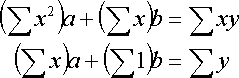
これを解くと,
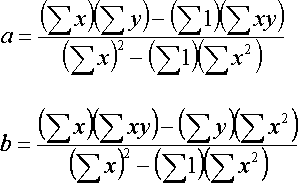
となる.
データ列(x,y)が与えられたとき,以下のEを最小化してa,b,cを求める問題を考えよう.
![]()
Eをa,b,cそれぞれで偏微分して=0とおいて得られる連立方程式は,
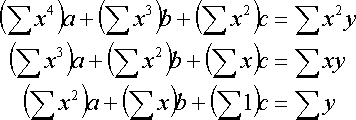
となる.これを解くと,
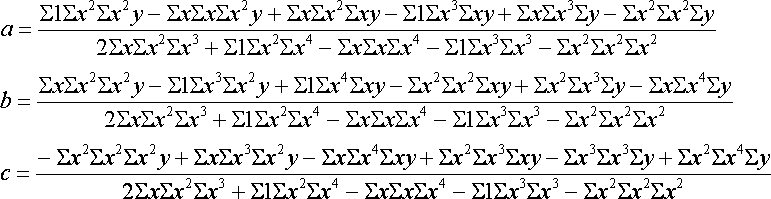
となる.ここで,
![]()
は,
![]()
の略である.その他の記号に関しても同様である.
一般の三角関数の場合は,非線形であるため,陽に求めることは(たぶん)できない.Levenberg-Marquardt法などの反復計算で求めるしかない.
周期が既知の三角関数の最小二乗問題は陽に解くことができる.
mを既知として,データ列(x,y)が与えられ,そのデータ列にy=Asinm(x-B)+Cを当てはめたい.そのためにA,B,Cを求めたい.この式をそのまま最小二乗法で解こうとしても,非線形であるため(たぶん)解くことはできない.そこで,以下の三角関数の性質を利用する.
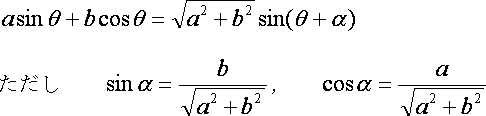
つまり,
![]()
の最小2乗問題は解くことができる.そこで,
![]()
を最小2乗法で解き,a,b,cを求め,それをA,B,Cに変換すれば良い.
a,b,cは以下の通りになる.
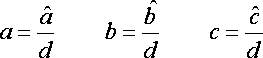
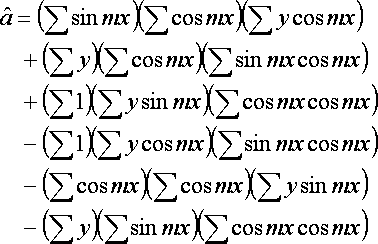
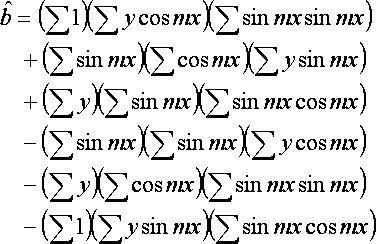
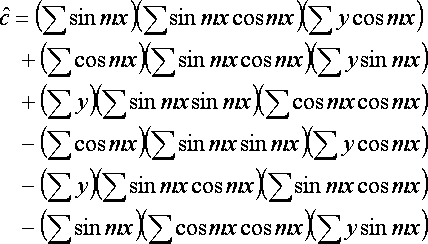
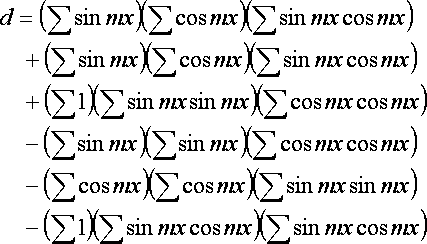
a,b,cからA,B,Cに変換するには,以下のように計算する.
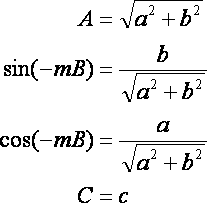
ちょっと待て!本当にこれで求まるのか?位相Bを求めるのに曖昧性があるじゃないか!周期の整数倍を足したり引いたりしたものもBの推定値としてありえるじゃないか!しかも,Bによって,Aの値の正負の曖昧性もあるだろう!線形最小二乗法で安定に解けるはずがない!
・・・とお思いの方も多いかと思います.ご心配なく.その点は問題ありません.この方法でちゃんと安定してパラメータを求めることができます.
この方法のミソは,y=Asinm(x-B)+Cを直接当てはめるのではなく,y=asinmx+bcosmx+cを当てはめることなのです.y=asinmx+bcosmx+cを最小二乗法で解くと,a,b,cが一意に定まります.
では,その証明を示しましょう.知りたいのは以下の事になります.
(1) asinx+bcosx+c=a'sinx+b'cosx+c'
となるa≠a'かb≠b'かc≠c'が存在するか?
もし,これが存在するなら,a,b,cの候補として複数あることになります.すなわち,パラメータを求めるのに曖昧性が存在することになります.(1)を変形すると,
(2) (a-a')sinx+(b-b')cosx+(c-c')=0
となります.第1項と第2項は,前述したように一つの三角関数で表せます.
(3) ![]()
ただし,
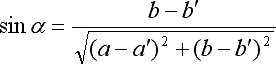
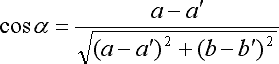
sin関数はxに応じて-1~1の値を取るので,全てのxについて(3)を成り立たせるためには,sin関数の係数が0でなければなりません.よって,
(4) ![]()
(5) ![]()
が両方成り立たなければなりません.よって,c=c'となります.また,
(6) (a-a')2+(b-b')2=0
ですが,(a-a')2も(b-b')2も0以上の値であるため,この式を満たすのは,(a-a')2=0かつ(b-b')2=0のときのみです.すなわち,a=a',b=b'となります.
以上で,a,b,cは一意に求まることが分かりました.a,b,cからA,B,Cを求めるのは,前述した変換式を使います.この変換式では,Aは0以上の値に必ずなります.また,Bは周期に応じた曖昧性がありますが,ユーザの自由に,ユーザの求めたい範囲で,求めることができます.
ちなみに,上の証明ですが,(2)からすぐに,a=a',b=b',c=c'が導けます.わざわざ一つの三角関数にしたのは,「もし,cosx=sinx+?みたいな形に変形できたらa,b,cは一意にならないぞ」と思う人がいるかもしれないことを考えてのことです.そのような変形はできないのでご安心を.