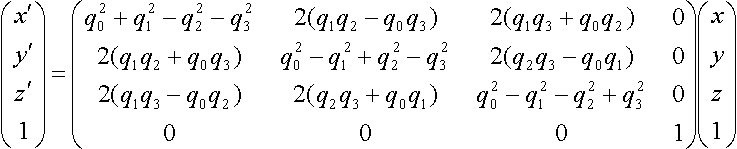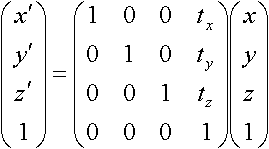
3次元図形変換の行列表現について解説する.特に,3次元空間における回転行列の表現方法を紹介する.回転行列は3×3行列で表現され,オイラー角で表した行列やクォータニオンで表した行列やロドリゲスの公式で表した行列などがある.x軸周りの回転行列,y軸周りの回転行列,z軸周りの回転行列なども紹介する.
平行移動
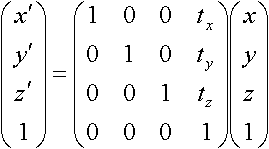
拡大・縮小、反転
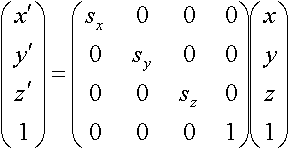
x軸まわりに角度αだけ回転した場合
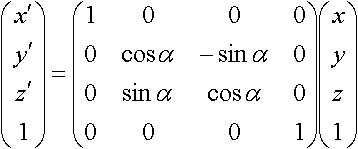
y軸まわりに角度βだけ回転した場合
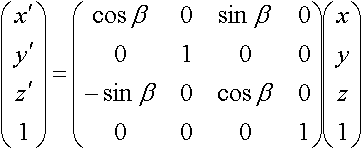
z軸まわりに角度γだけ回転した場合
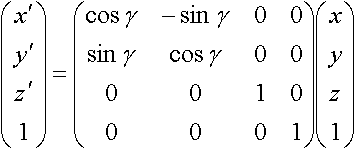
Euler角αβγで回転する場合
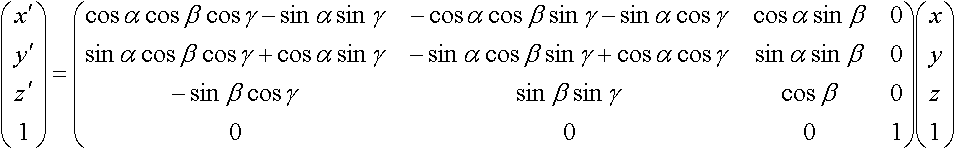
ロール(φ)ピッチ(θ)ヨー(ψ)で回転する場合
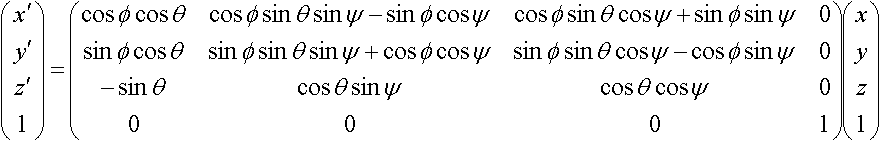
ベクトルの方向=回転軸,ベクトルの長さ=回転量で回転する場合(ロドリゲスの公式)
正規化されていないベクトルをv=(vx,vy,vz)、回転量をθ=|v|とする。
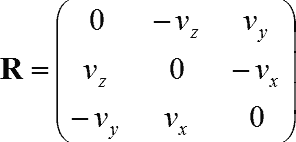
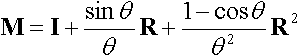
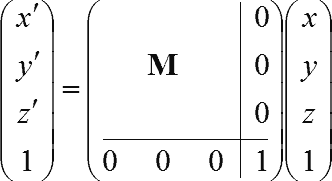
θが0に近い場合.
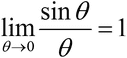

任意の単位ベクトル(vx,vy,vz)まわりにθ回転する場合(ロドリゲスの公式)
単位ベクトルv=(vx,vy,vz)を回転軸、回転量をθとする。
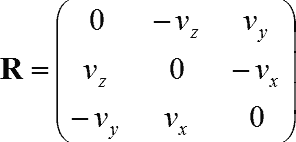
![]()

任意の単位ベクトル(nx,ny,nz)まわりにθ回転する場合
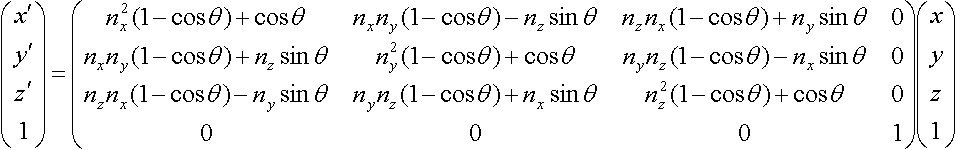
4元数(Quaternion)で回転する場合
4元数をq=(q0,q1,q2,q3)とし、|q|=1を満たすものとする。